第10号　教えて先生！クイズ

もんだい

高さの低い容器を用意します. この容器に粘りけのある液体(例えば水飴)を満たし, 容器の中に3本の棒を差し込みます (Figure 1(1)). Figure 1(2)は容器を上から見た図です. 容器の中に染料を少し入れてから, 次の操作Aと操作Bの2つの実験を行います.

閉じる

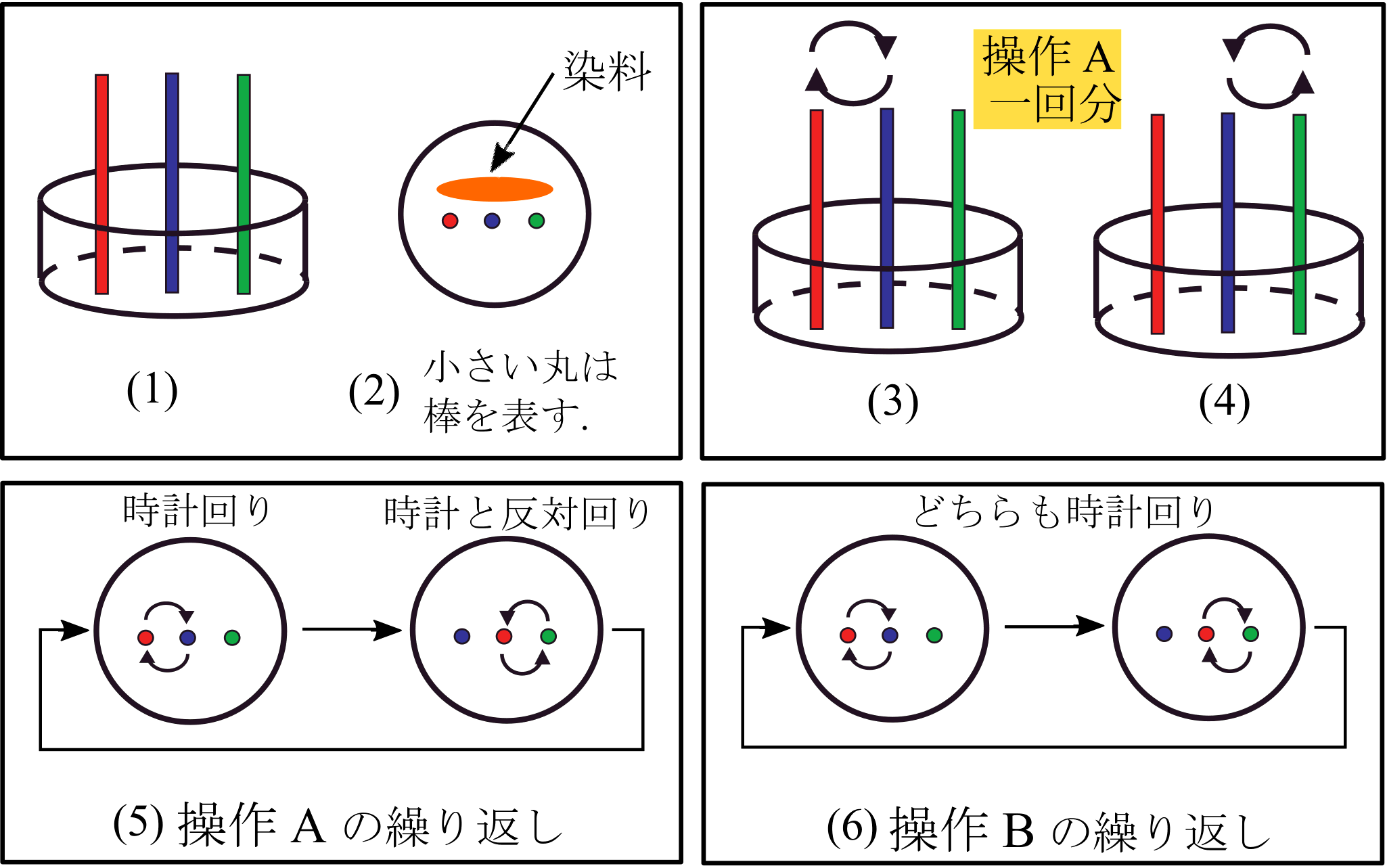
Figure 1. (1) 容器. (2) 容器を上から見た図. (3)と(4) 操作Aの1回分. (5) 操作Aの繰り返し. (6)操作Bの繰り返し.

操作A. 左にある棒と真ん中にある棒を時計回りに入れ替える(Figure 1(3)). 次に真ん中にある棒と右にある棒を時計と反対回りに入れ替える(Figure 1(4)). ここまでが操作Aの一回分です.

操作B. 左にある棒と真ん中にある棒を時計回りに入れ替える. (これは操作Aと同じ.) 次に真ん中にある棒と右にある棒を時計回りに入れ替える. (つまり棒の入れ替えは時計回りのみ.) ここまでが操作Bの一回分です.

操作Aと操作Bのそれぞれの繰り返しによって染料がどのように混ざるのか観察します(Figure 1(5)(6)). ゆっくりと棒を入れ替えればどのような結果が得られるでしょうか? 次から選んでください.

操作Aの方がよく混ざる.
操作Bの方がよく混ざる.
混ざり方には差はない.

こたえ

正解は 1 です. 物質や液体を効率的に均一にかき混ぜることは様々な応用があります. この実験を提案したのは Boyland, Aref, Stremler の3人です. 論文 [1] には実験結果の写真が掲載されています. 単純ですが数学のトポロジーとミキシングの研究を結びつけた画期的な実験だと思います. トポロジーは柔らかい幾何学と言われることがあります. ドーナッツとマグカップはトポロジーの観点では同じです.

閉じる

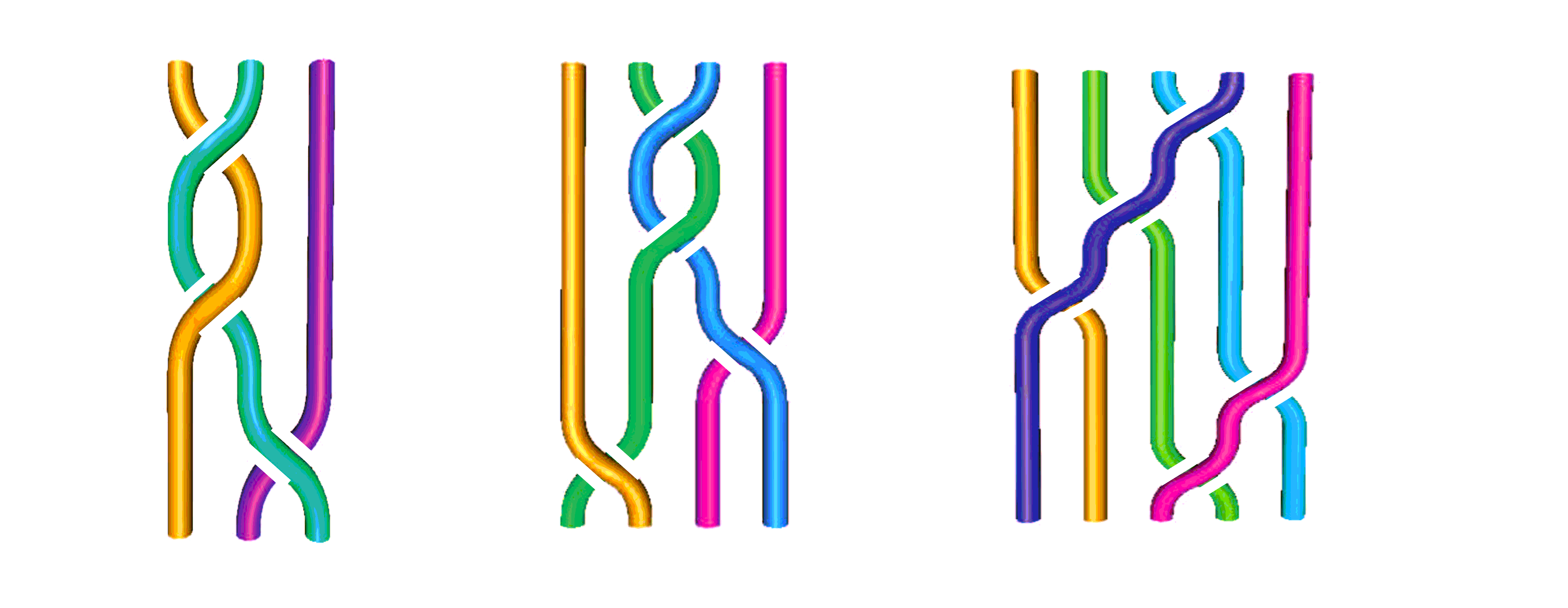
Figure 2. いろいろな組ひも. 3本の組ひも, 4本の組ひも, 5本の組ひもの例.

なぜトポロジーと関係があるのでしょうか?
　(い)高さの低い容器
　(ろ)粘りけのある液体
　(は)ゆっくりとした棒の入れ替え
がキーワードです. 容器は立体ですが(い)より2次元の円板 (Figure 1(2))とみなします. 容器を上から見ると3本の棒は円板の中の3点です. (ろ)(は)より2本の棒の入れ替えは円板の3点のうちの2点の入れ替えと見なすことができます. 点の入れ替えに従って3点が動く軌跡を3次元空間に描くと3本の組ひも α が得られます (Figure 3の左図). 因みに「組ひも」は数学用語です. Figure 2は組ひもの例です.

閉じる

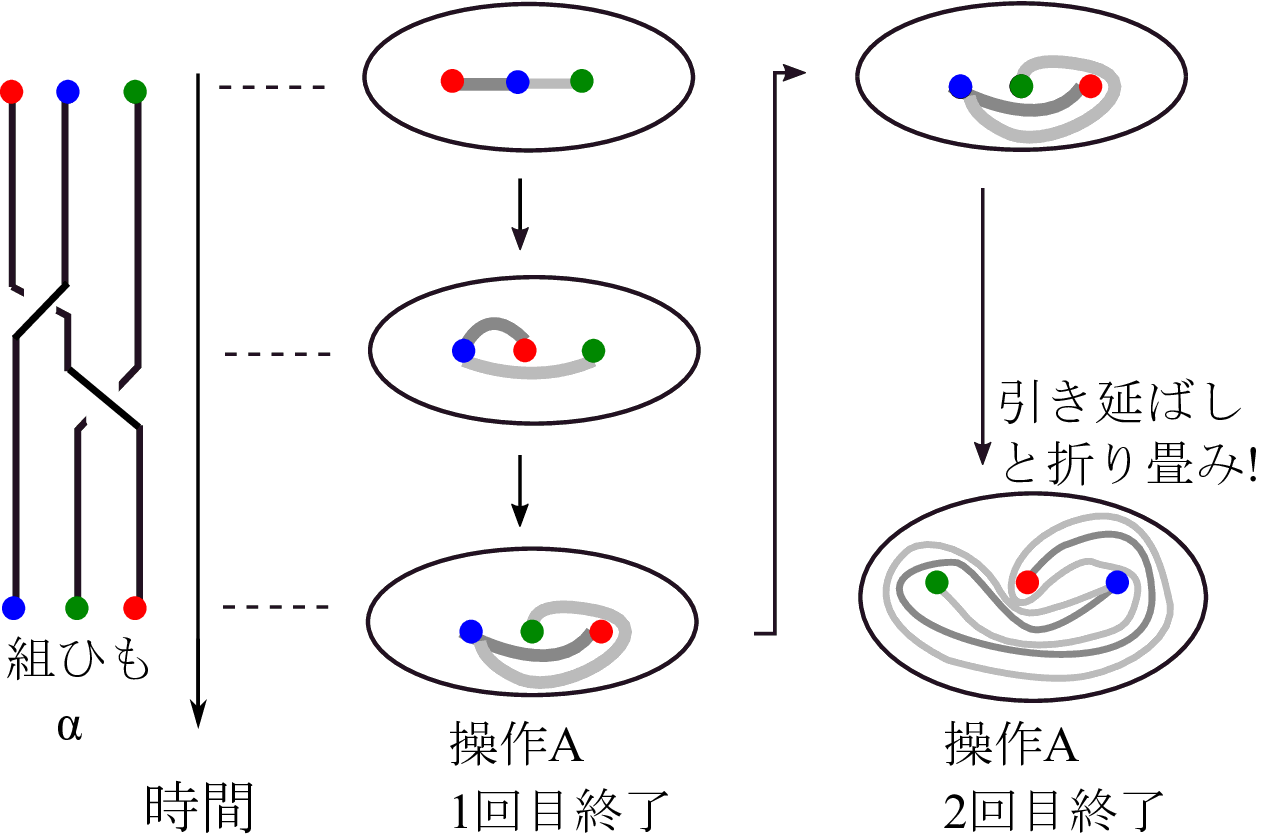
Figure 3. 左図は操作Aから定まる組ひも α. 3点を結ぶ線(濃いグレーと薄いグレー)は操作の繰り返しによって複雑になっていく.

同様に操作B から3本の組ひも β が定まります (Figure 4の左図). 組ひも α と β は似ていますが違うところが１箇所あります. 組ひも α や β が, 操作A や操作B のかき混ぜの性質を捉えているのです.

閉じる

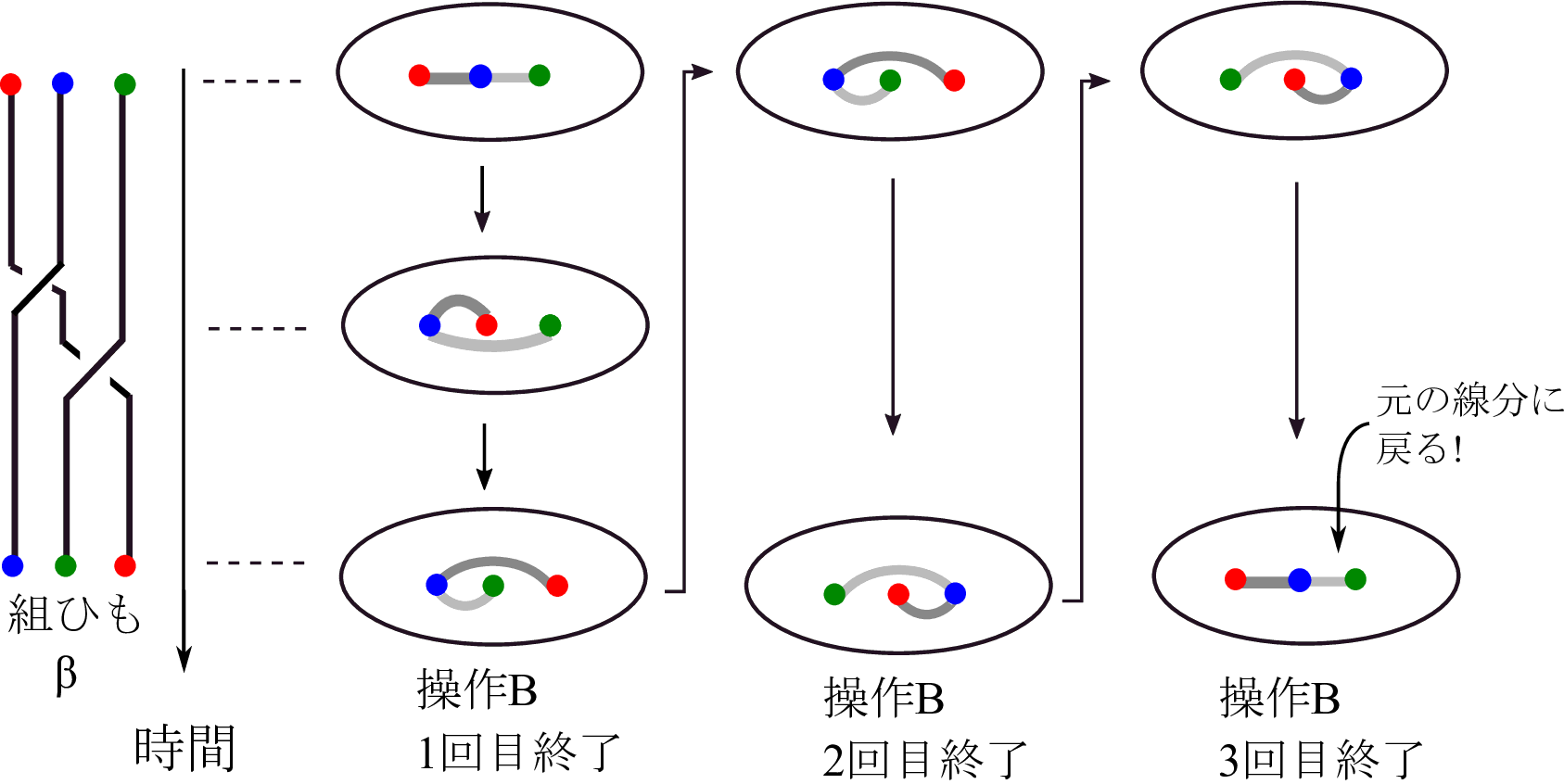
Figure 4. 左図は操作Bから定まる組ひも β. 3点を結ぶ線(濃いグレーと薄いグレー)は操作を3回繰り返すと元の線に戻ってしまう.

ここで用語の準備をします.

同じ組ひもとは? 二つの組ひも X と Y が同じとは, 組ひも X の両端の点を固定したまま X を3次元空間の中で変形することによって組ひも Y にできることです. 途中でひもが交わってはいけません. Figure 5は見かけは違いますが同じ組ひもを表しています.

閉じる

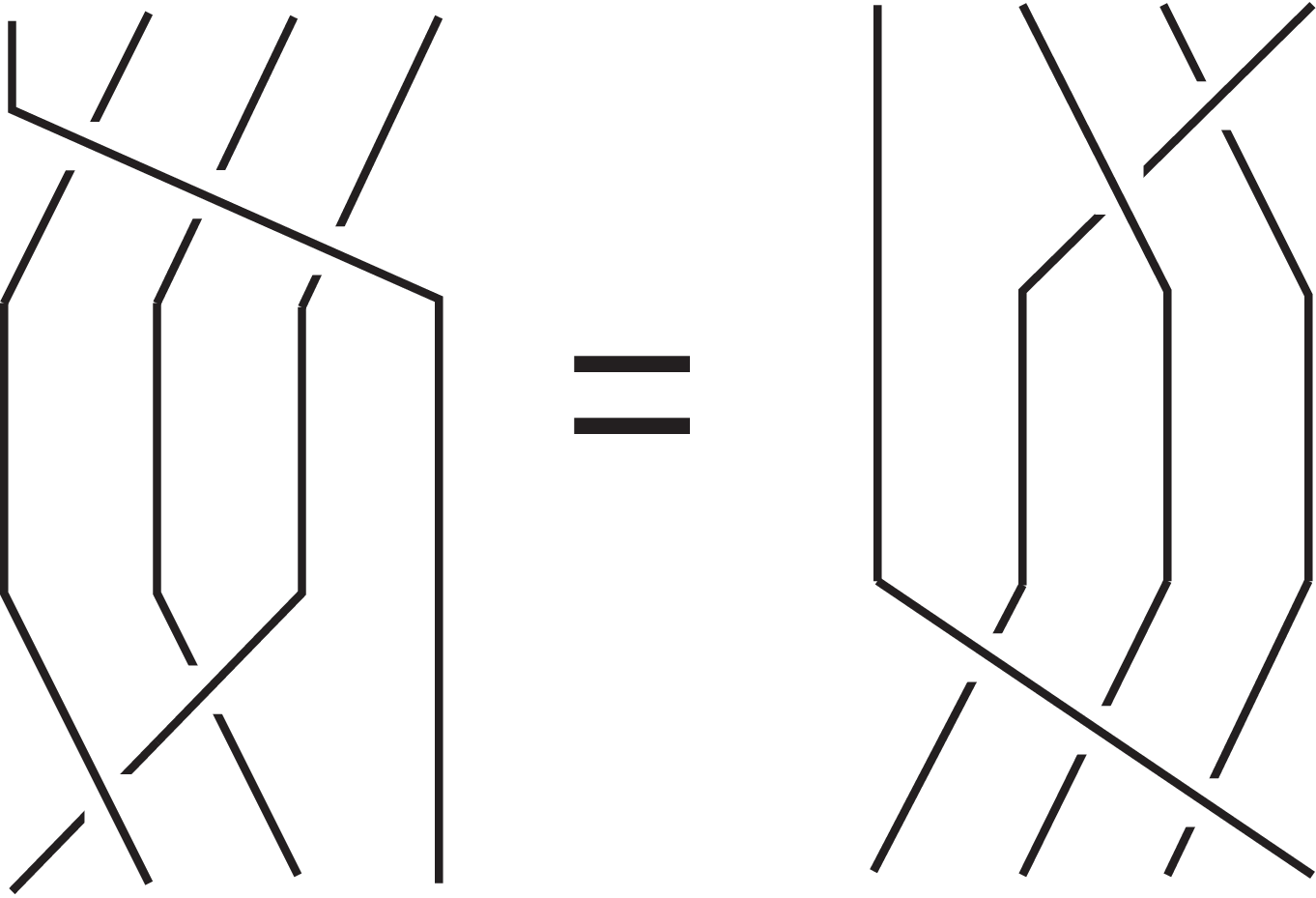
Figure 5. 同じ組ひもを表す.

組ひもの分類. 組ひもには3つのタイプがあります.

擬アノソフ型
周期型
可約型

簡単にいうと擬アノソフ型は複雑な性質を持つ組ひもであり, 周期型は単純な性質を持つ組ひもです. 可約型は適当な分解をすれば周期型か擬アノソフ型の組ひもに帰着できる組ひものことです. 擬アノソフ型の組ひもには興味深い性質がたくさんあります. 実は操作A の組ひも α は擬アノソフ型の例で, 操作B の組ひも β は周期型の例になっています.

組ひも α が擬アノソフ型であることと β が周期型であることが, 実験結果にどのような影響を与えるのでしょうか? これは直感的にはFigure 3, 4を見れば理解できます. 円板の上の3点を結ぶ線を引きます. この線が操作A や操作B の繰り返しによってどのように写るのか考えます. 操作Bでは, 3回の繰り返しによって最初の線に戻ってしまいます(Figure 4). かき混ぜたはずなのに, 初期の状態に戻ってしまうということ. これは困ります. 操作B では均一なかき混ぜが達成できないという結果が出るのですがその数学的な理由はこのことにあります.

一方, 操作A では何回か繰り返すと最初の線に戻ることは決して起こりません. それどころか, 繰り返しの回数とともに線は大きく引き伸ばされ, 複雑になっていきます (Figure 6). このことが, 操作A では均一なかき混ぜが達成できる理由です. 操作AやBの性質は, 組ひも α や β のみから定まることが重要なポイントです.

最後に, Figure 6 は本稿で取り上げた実験と類似の設定の数値計算の結果 [2] です. 棒に相当する3点の近くに沢山の点をプロットし, かき混ぜによってどのように散らばるのか調べています. Figure 6の (1) は操作Aに, Figure 6の (2) は操作Bに対応すると考えてください. (1) の方が (2) よりも均一に広い範囲において点が散らばっていることがわかります.

閉じる

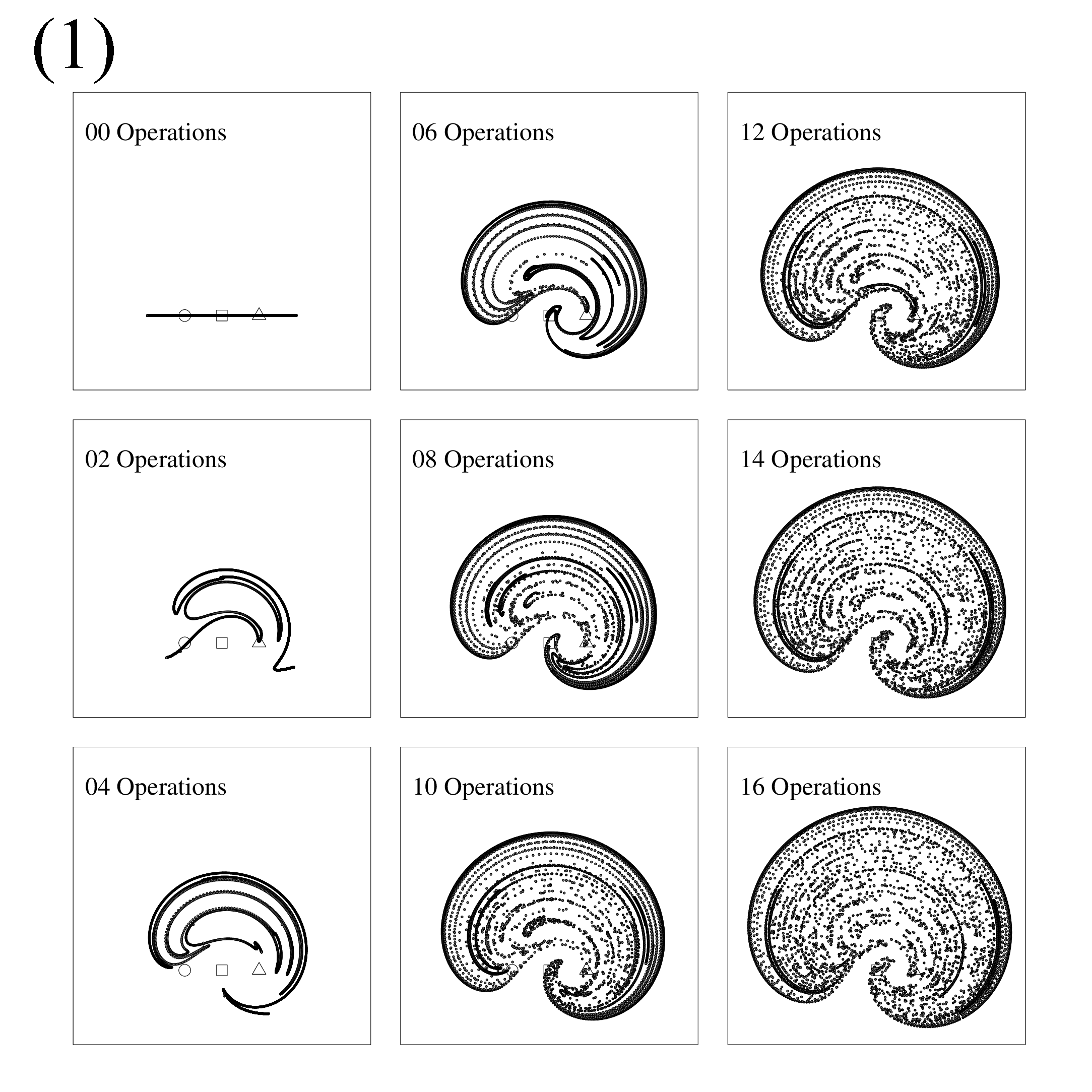
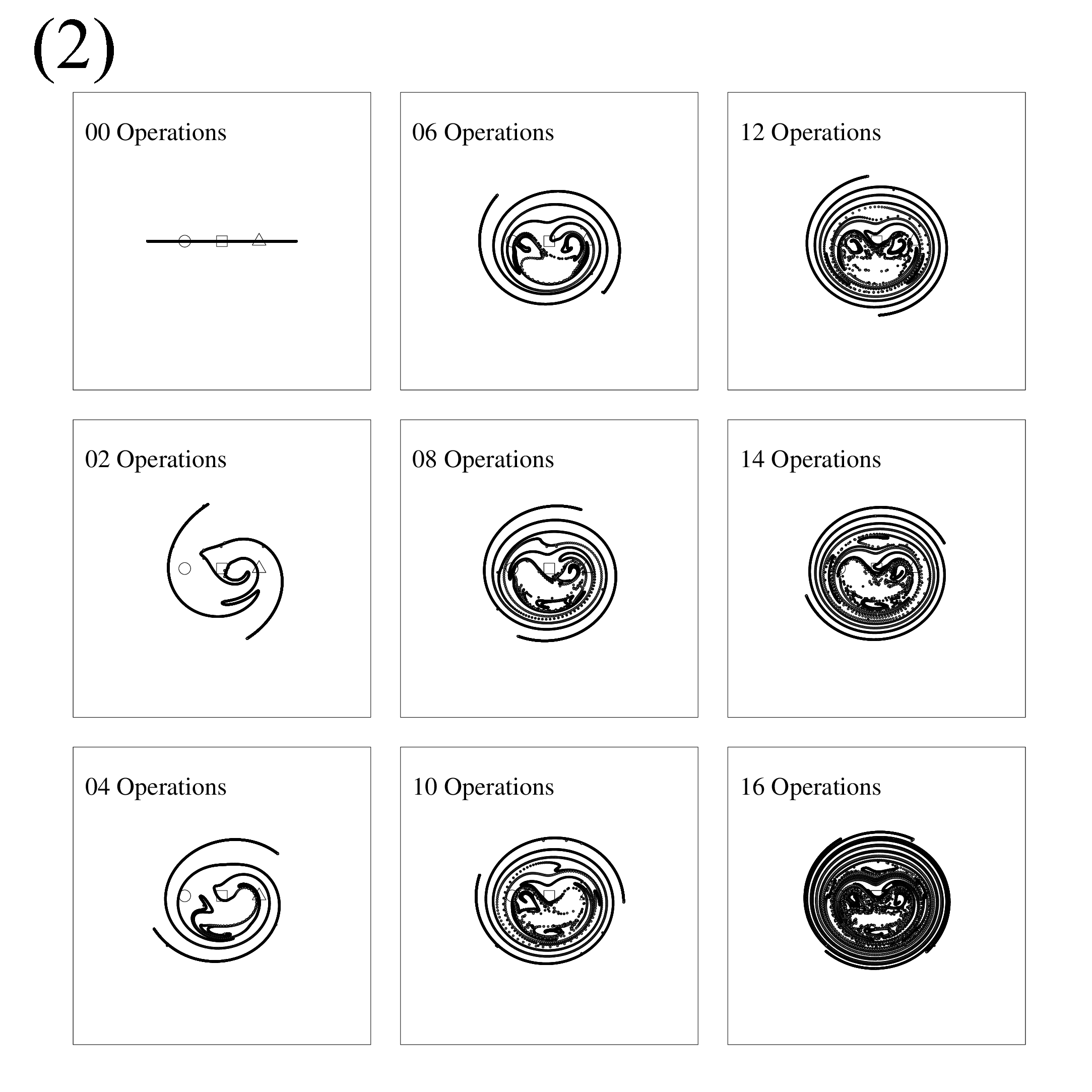
Figure 6. 坂上貴之氏(京都大学)による数値計算の結果 [2]. (1) が操作Aの実験結果に相当するもの. (2) が操作Bの実験結果に相当するもの.

References

[1] P. Boyland, A. Hassan and M. Stremler, Topological fluid mechanics of point vortex motions, Phys. D, 175 (2003), no. 1-2, 69--95.
[2] E. Kin and T. Sakajo, Efficient topological chaos embedded in the blinking vortex system, Chaos 15, (2005), no. 2, 023111, 9.